Peridynamic Unit Cell
An efficient and accurate simulation tool of composite micro-structures.
About
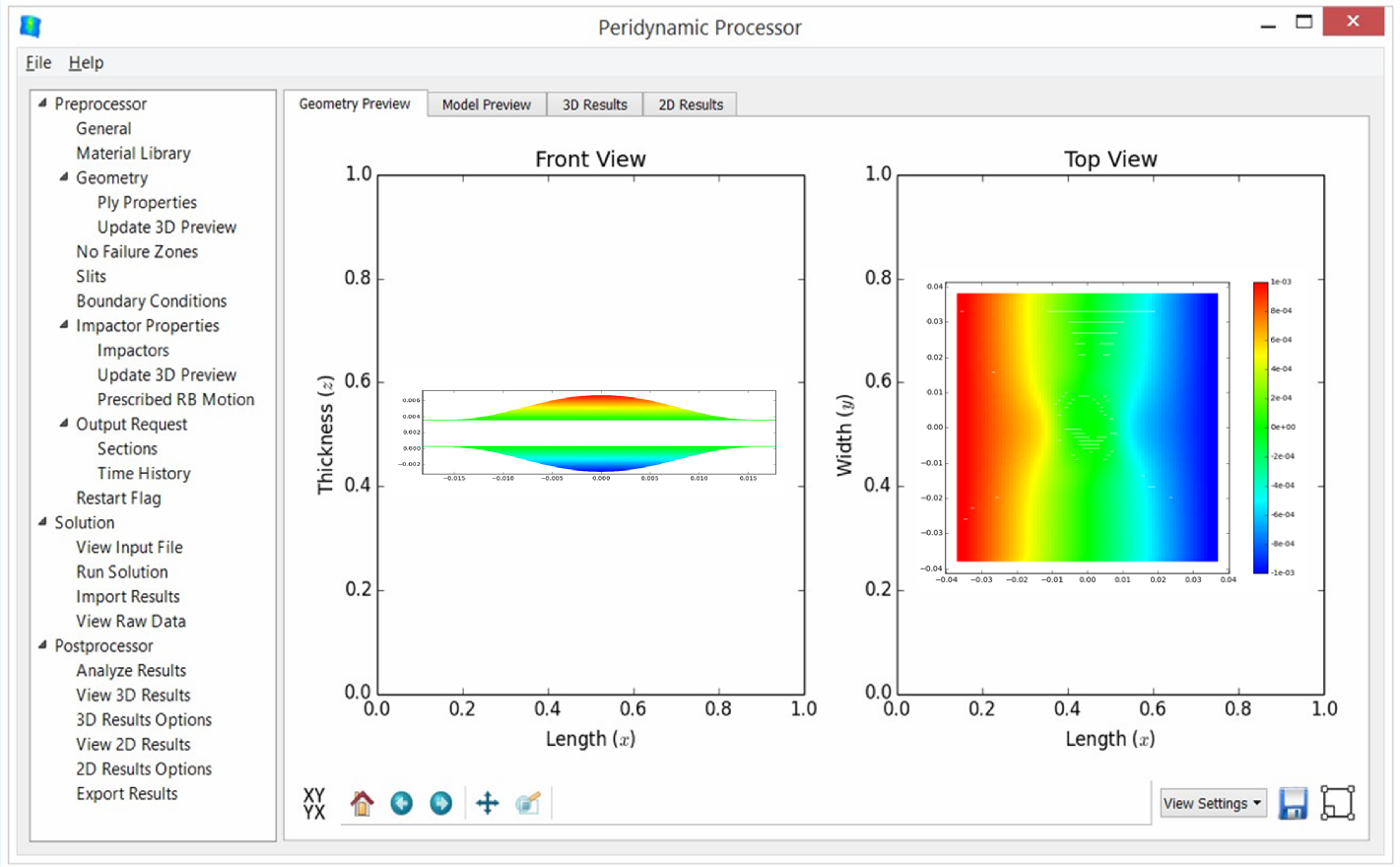
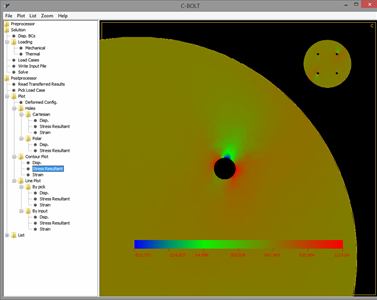
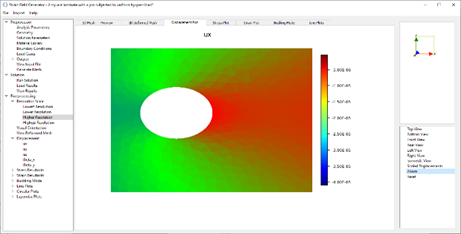
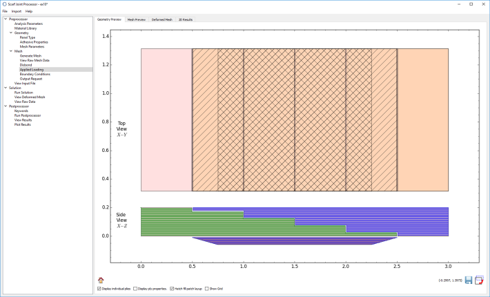
Peridynamics Unit Cell, written in Python and C++, is a homogenization tool for predicting effective thermoelastic properties of micro-structures. In PDUC, normal and shear deformations are identified via normal and shear bonds, respectively. The normal bonds are perpendicular to each other and aligned with the axes of a Cartesian coordinate system. The shear bonds are off-axes and only lie on the three orthogonal planes of the coordinate system. The family or interaction domain is naturally a cube or a square depending on the dimension of the analysis.
Contact Us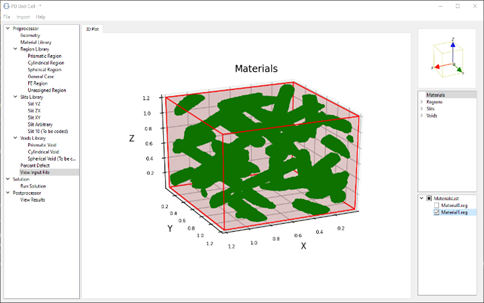
In Peridynamics Unit Cell (PDUC), the constituent materials such as fiber and matrix can be modeled as orthotropic materials. Also, the number of constituents can be arbitrary. Voids and cracks can be modeled by breaking the bonds between the material points. The bond breakage can be modeled to represent random damage-nucleation sites. The periodic boundary conditions are applied in a natural way without any constraint conditions. It enables the determination of fully anisotropic stiffness matrix of a complex microstructure in the presence defects such as cracks, voids, and heterogeneity such as dissimilar reinforcement material in the structure. Effective material property matrix, and damage matrix are computed for a heterogeneous micro-structure which includes matrix cracks and debonds along the fiber-matrix interface. Currently, PDUC is compatible with Ansys. The element and node information generated by Ansys can be imported to PDUC.
Features
- Highly hetergenous microstructural topology
- User-friendly Graphical user interface
- Custom 3D rendering engine
- Various display styles (scatter, cube, solid, wire)
- Interactive results plots
- Data manipulation
- Scalar and extent clipping
- Exaggerated deformed shape
- Layer splitting
- Animation of results
- General loading and boundary conditions
- Material anisotropy
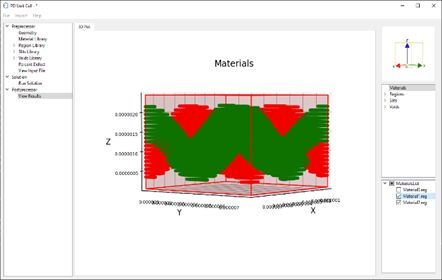

Capabilities
- Custom materials: Isotropic and Orthotropic
- Multiple failure criteria: Fiber, Matrix, and Interply
- Pre-existing cracks
- Force and displacement boundary conditions
- Various projectile shapes: Sphere, ogive, cylinder, etc.
- Internal force calculation
- Time history tracer points
All Products